Блог им. Sergey_gt |Богатеем медленно (Часть 3, и последняя)
- 23 июля 2016, 11:38
- |

Продолжение. Начало здесь.
Эксперименты
Но как же изменится среднее отклонение оптимизированного портфеля за пределами выборочного контроля, по сравнению с с 1/N? Ниже приведен скрипт для проведения экспериментов с различными структурами портфеля, периодами возврата, ограничениями значений и отклонениями:
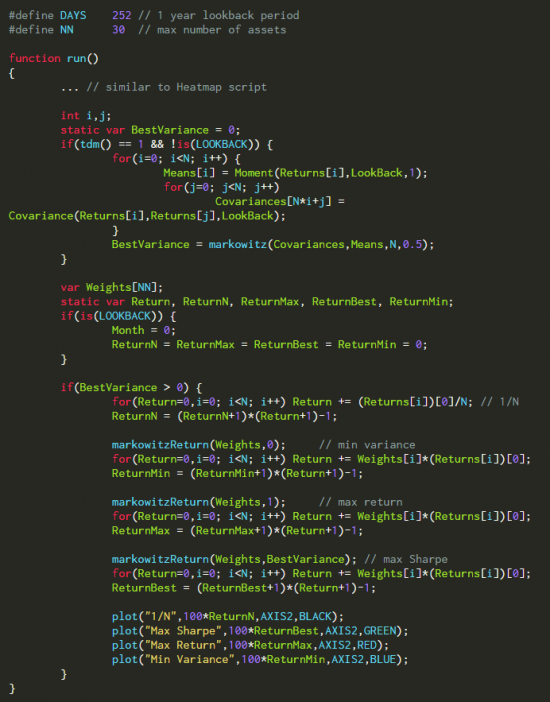
( Читать дальше )
- комментировать
- ★18
- Комментарии ( 14 )
Блог им. Sergey_gt |Богатеем медленно (Часть 1)
- 19 июня 2016, 12:22
- |

Большинство трейдинговых систем относятся к типу тех, на которых можно разбогатеть быстро. Они используют временную низкую производительность рынка и стремятся к ежегодным прибылям в 100% областей. Они требуют постоянного контроля и адаптации к условиям рынка, но даже при этом имеют ограниченное срок службы. Их истечение срока действия часто сопровождается большими потерями. Но что если вы, тем не менее, собрали некоторые привлекательные прибыли, и теперь хотите перенести их в более безопасное и надежное место? Положить деньги под подушку? Отнести их в банк? Вложить в хедж-фонды? Очевидно, что все это идет вразрез с кодексом чести алготрейдера. Так что вот вам альтернатива.
Старомодный метод инвестирования предполагает покупку некоторого количества низкорисковых акций и длительное ожидание. У любого портфеля акций есть определенный средний возврат и определенное колебание значений; обычно вы хотите минимизировать последний и максимизировать первый. Оптимальное распределение капитала среди компонентов портфеля производит или максимальный средний возврат для данного позволенного колебания, или минимальное колебание – соответственно, минимальное расхождение – для данного среднего возврата. Это оптимальное распределение часто очень отличается от инвестирования той же суммы во все N-компоненты портфеля. Простой способ решения этого среднего значения / расхождения оптимизации был опубликован 60 лет назад Гарри Марковицем, за что он позже получил Нобелевскую премию.
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- си
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















